티스토리 뷰
1. 변수
- 변수 : 각 단위에 대해 관측되는 특성 ( ex. 성별, 나이, 학력 등 )
- 데이터 : 하나 이상의 변수에 대한 관찰값의 모음
2. 변수의 종류
- 질적 변수( Qualitative Variable 범주형 변수 )
- 유한개의 범주 중 하나의 값을 취하는 변수 ( ex. 성별, 학력 )
- 종류
- 명목형 변수( Nominal Variable ) : 범주들에 의미 있는 순서를 정할 수 없는 질적 변수 ( ex. 성별 )
- 순서형 변수( Ordinal Variable ) : 범주 간의 의미 있는 순서를 정할 수 있는 질적 변수 ( ex. 학력 )
- 양적 변수( Quantitative Variable )
- 양적인 수치로 측정되는 변수 ( ex. 나이, 몸무게 )
- 종류
- 연속형 변수( Continuous Variable) : 어떤 실수 구간 안의 모든 값을 가질 수 있는 변수 ( ex. 몸무게 )
- 이산형 변수( Discrete Variable ) : 취할 수 있는 값을 셀 수 있는 양적 변수 ( ex. 나이 )
3. 변수의 분포
- 변수의 데이터에는 변동( Variability )이 있다
- 변수의 분포는 변수가 취할 수 있는 모든 값에 대해 각 값이 발생하는 빈도를 나열한 것
- 도수분포표( Frequency Table )
- 데이터에서 각 값의 출현빈도나 비슷한 값끼리 묶은 구간별로 관측된 데이터의 개수를 정리한 표
- ex ) 한 학급의 학생들의 혈액형 분포, 한 학급의 학생들의 키 분포
4. 도수분포표 만드는 법
- 질적 변수의 경우
- 각 범주에 속하는 단위의 개수를 제시
- 양적 변수의 경우
- 계급을 정한 후 각 계급에 속하는 단위의 개수를 제시
- 계급은 임의로 정할 수 있으나, 각 계급의 폭을 일정하게 하는 것이 좋다
- 계급의 폭이 너무 좁을 경우 계급의 개수가 너무 많아지거나, 각 계급의 도수가 너무 작아진다
- 계급의 폭이 너무 넓을 경우 전체적인 분포가 잘 드러나지 않을 수도 있다
- 각 계급의 경계점에 놓이는 관찰값의 개수가 적어지도록 계급을 정하는 것이 좋다
5. 질적 데이터의 요약 : 막대 그래프
- 각 범주에 속한 관찰값의 개수 또는 비율을 막대의 길이로 나타낸 그래프
- 명목형 변수일 경우
- 큰 빈도부터 작은 빈도, 또는 작은 빈도부터 큰 빈도 순서로 정렬하면 좋다
- ex ) 어느 학급 학생들의 등하교 교통수단
- 순서형 변수일 경우
- 범주의 순서를 지켜서 그리는 것이 좋다
- ex ) 어느 의원 환자들의 비만도 분포
6. 질적 데이터의 요약 : 원 그래프
- 각 범주에 속한 관찰값의 비율의 원의 면적으로 표현한 그래프
- 막대그래프에 비해서 정보 파악이 어렵기 때문에, 최근에는 선호되지 않는다
- ex ) 어느 학급 학생들의 등하교 교통수단
7. 양적 데이터 요약하는 방법
- 히스토그램, 점도표, 상자그림
- 평균, 표준편차, 분산
- 중앙값, 사분위수 범위
8. 양적 데이터의 요약 : 히스토그램 ( Histogram )
- 도수분포표를 그래프로 나타낸 것
- 계급을 수평축에 표시
- 각 계급의 도수에 비례하는 넓이의 직사각형
- ex ) 어느 학급의 영어점수 분포를 나타낸 히스토그램
9. 히스토그램과 특이점
- 히스토그램을 이용하면 특이점을 쉽게 찾을 수 있다
- 특이점( Outlier ) : 대부분의 데이터로부터 멀리 떨어져 있는관찰값
10. 히스토그램과 분포
- 히스토그램을 이용하면 전체적인 분포를 한눈에 파악할 수 있다
- 주의점 : 같은 데이터라도 계급의 폭에 따라 분포의 특성이 달라보일 수 있다
11. 분포 유형
- 종 모양 분포( Bell-shaped Distribution ) : 좌우 대칭이고 데이터가 가운데에 모여있다
- 쌍봉우리형 분포( Bimodal Distribution ) : 2개의 봉우리 주변으로 데이터가 모여있는 분포
- 치우친 분포( Skewed Distribution): 비대칭으로 한쪽 꼬리가 다른 쪽 꼬리보다 긴 분포
- 왼쪽으로 치우친( Right-skewed ) 분포 : 오른쪽 꼬리가 더 길다
- 오른쪽으로 치우친( Left-skewed ) 분포 : 왼쪽 꼬리가 더 길다
- 균등분포( Uniform Distribution): 어떤 범위 내의 값이 고르게 나타나는 분포
12. 양적 데이터의 요약 : 점도표
- 수평선 위에 데이터 값에 해당하는 위치에 점을 찍는 그래프
- 데이터가 적을 때 유용하다
- 관찰값의 개수가 20~30개를 넘어가면 너무 복잡해진다
13. 양적 데이터의 요약 : 최빈값( Mode )
- 관찰값 중에서 발생빈도가 가장 높은 값
- 여러개일 수도 있고, 하나도 없을 수도 있다
14. 양적 데이터의 요약 : 무게 중심과 평균
- 점도표를 시소 위에 물체가 놓여있는 것으로 생각하면, 시소가 평형을 이루는 무게 중심의 위치가 데이터를 대표한다고 생각할 수 있다
- 평균( Mean )
- 양적 변수의 분포의 균형을 이루는 무게중심의 위치에 해당하는 값
- 어떤 변수의 관찰값의 총합을 관찰값의 개수로 나눈 값
15. 평균의 특징
- 표본데이터가 기울어진 분포를 가졌거나 특이점이 있는 경우, 평균이 데이터 전체를 잘 대표하지 못한다
- 특이점의 영향을 크게 받는다
- 데이터의 분포가 좌우 대칭인 경우 평균은 분포의 가운데에 위치한다
- 데이터 중 하나라도 한쪽으로 치우치면 평균은 특이점 쪽으로 움직이게 된다
16. 분산과 표준편차
- 편차 : 관찰값 – 평균
- 분산( Variance )
- 편차의 제곱의 평균
- 단, 평균을 낼때 데이터 개수 - 1개로 낸다. ( n-1 )
- 데이터가 중심으로부터 퍼져있는 정도를 나타냄
- 편차의 제곱의 평균
- 표준편차( Standard Deviatoin ) : 분산의 제곱근
- 특징
- 분산, 표준편차가 크면 데이터가 평균을 중심으로 광범위하게 분포되어 있다는 뜻
- 분산, 표준편차가 작으면 데이터가 평균을 중심으로 조밀하게 모여 있다는 뜻
- 분산, 표준편차는 특이점의 영향을 많이 받는다
- 분산의 단위 = 데이터 측정단위의 제곱
- 표준편차의 단위 = 데이터 측정단위
17. 변이계수 ( Coefficient Of Variation )
- 표준편차를 평균으로 나눈 값
- 변동을 비교할 때는 측정 단위나 데이터 중심위치의 차이를 고려해야 한다.
- ex ) 만 9세의 체중과 만 21세 체중의 표준편차
18. R 패키지 설치
- R 자체에 내장되지 않은, 사용자들이 개별적으로 만들어낸 함수들의 모음
- 누구나 새로운 패키지를 만들어서 공유할 수 있다
- CRAN에서 Packages > Table of available packages, sorted by name을 선택하면 공개된 모든 패키지를 볼 수 있다
19. ggplot2 패키지
- Wilkinson의 The grammar of graphics의 원칙에 따라 그래프를 만들 수 있는 함수들의 모음
- 기본 구조에 레이어를 추가하는 방식으로 원하는 그래프의 형태를 지정한다
- 디테일을 상세하게 지정하지 않아도 자동으로 예쁜 그래프를 그려준다
20. R 패키지 설치하는 방법
- R Studio의 오른쪽 아래 Packages 창에서 원하는 패키지 이름 검색 후, 체크박스 선택하고 Install 클릭하기
- R Studio의 위쪽 메뉴에서 Tools>Install Packages 메뉴를 선택하고 대화창에 원하는 패키지 이름 입력, Install 클릭하기
- 콘솔에 install.packages(“원하는 패키지 이름”) 입력
21. 패키지 로드
- 패키지를 설치한 후, 반드시 ‘로드( load )’해야 사용할 수 있다
- 로드하는 명령어 : library(ggplot2)
- 한번 설치한 패키지는 ( 일부러 지우거나 R을 업그레이드 하지 않는 한 ) 없어지지 않으므로 재설치가 필요없다
- 한번 로드한 패키지는 R Studio를 닫으면 주기억장치에서사라진다.
- 따라서 R Studio를 닫았다가 다시 열 경우, 필요한 패키지를 다시 로드해야 한다
- 패키지를 로드하는 명령어를 스크립트에 저장하는 것이 좋다
22. ggplot2 이용하여 그래프 그리기
- 기본 형태
- ggplot( data = <DATA> ) + <GEOM_FUNCTION>( mapping = aes(<MAPPINGS>))
- ggplot은 그래프를 그릴 데이터셋을 지정
- GEOM_FUNCTION에는 그리고자 하는 그래프 함수를 지정하고
- aes에는 x축과 y축 설정을 하면 된다.
- ggplot( )은 먼저 자료의 좌표축을 만든다
- geom function은 mapping = aes() 구문을 통해 x축과 y축 변수를 지정한다
- 그래프의 종류에 따라 다른 geom function을 사용한다
- 주의: “+”는 항상 라인의 마지막에 위치해야 한다
23. ggplot2 사용 예제 1
library(ggplot2)
transp <- c ("bicycle", "bus", "walking", "bicycle", "bicycle", "bicycle", "bus")
data1 <- data.frame(transp)
View(data1)
// 막대그래프
// xlab 함수는 x축 라벨 변경시 사용
ggplot(data = data1) + geom_bar (mapping = aes(x = transp)) +
xlab("Transportation")
24. forcats 사용 예제 1
- forcats 사용시 빈도수에 따라서 막대 그래프가 생성된다.
- 빈도수가 높은 -> 낮은 순으로 나타난다.
ggplot(data = data1) + geom_bar (mapping = aes(x = fct_infreq(transp))) +
xlab("Transportation")25. ggplot2 사용 예제 2
- levels를 통해 factor에서 지정한 범주형 변수의 순서를 정할 수 있다.
besity<-factor(c("underweight", "normal", "overweight", "obese"),
levels=c("underweight", "normal", "overweight", "obese"))
count<-c(6, 69, 27, 13)
perc<-count/sum(count)*100
dat2<-data.frame(obesity, count, perc)
ggplot(data=dat2) + geom_bar(mapping=aes(x=obesity, y=perc),
stat="identity") + xlab("Obesity") + ylab("Percentage (%)")
26. ggplot2 사용 예제 3 : 원 그래프
- 원 그래프 사용 시, x 축에는 “”를 입력해야 한다.
- stat에는 identity를 입력해야 한다.
table(transp)
dat3<-data.frame(transportation=c("bus", "bicyle", "walking"), count=c(15, 13, 4))
ggplot(data=dat3) + geom_bar(mapping=aes(x="", y=count, fill=transportation),
stat="identity") +
coord_polar("y", start=0) + xlab("") + ylab("")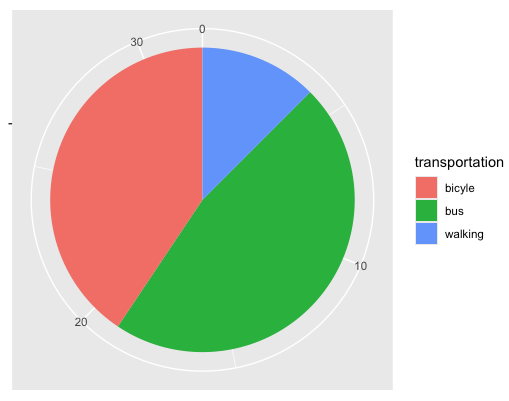
27. ggplot2 사용 예제 4 : 원 그래프 2
- 원 그래프의 보조축을 나태내지 않는 방법
ggplot(data=dat3) + geom_bar(mapping=aes(x="", y=count, fill=transportation),
stat="identity") +
coord_polar("y", start=0) + xlab("") + ylab("") +
theme(axis.text = element_blank(),
axis.ticks = element_blank(),
panel.grid = element_blank())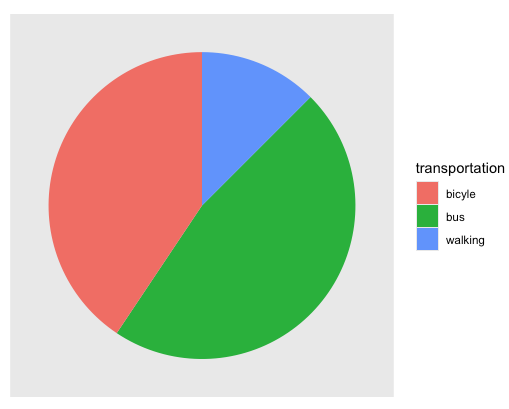
28. 요약
- 변수는 질적 변수와 양적 변수로 나뉜다.
- 질적 변수에는 명목형 변수, 순서형 변수가 있다.
- 양적 변수에는 연속형 변수와 이산형 변수가 있다.
- 변수의 분포를 나타내기 위하여 각 값의 출현빈도나 비슷한 값끼리 묶은 구간별로 관측된 데이터의 개수를 정리한 표를 도수분포표라고 한다.
- 막대그래프, 히스토그램, 점도표를 이용하여 데이터를 요약할 수 있다.
- 특이점은 대부분의 데이터로부터 멀리 떨어져있는 관찰값이다.
- 평균은 분포의 무게 중심으로서 관찰값의 총합을 표본크기로 나눈 값이다.
- 분산은 편차의 제곱의 평균이고, 표준편차는 분산의 제곱근이다.
728x90
'방송대 > 통계학계론' 카테고리의 다른 글
| 7강. 확률분포와 표본분포 (2) (0) | 2025.04.09 |
|---|---|
| 6강. 확률분포와 표본분포 (1) (0) | 2025.04.01 |
| 5강. 확률 및 확률 분포 함수 (2) (0) | 2025.03.23 |
| 4강. 확률 및 확률분포함수 (1) (0) | 2025.03.15 |
| 1강. 데이터와 통계학 (0) | 2025.02.20 |
댓글
