티스토리 뷰
1. 데이터 요약 방법
- 질적 데이터 요약
- 막대 그래프
- 양적 데이터 요약
- 히스토그램
- 점도표
- 평균, 분산, 표준편차
- 상자 그림
- 중앙값, 사분위수 범위
2. 평균의 특징
- 데이터의 분포가 좌우 대칭인 경우 평균은 분포의 가운데에 위치한다
- 데이터 중 하나라도 한쪽으로 치우치면 평균은 특이점 쪽으로 움직이게된다
3. 중앙값 ( Median )
- 데이터를 크기 순서대로 늘어놓았을 때 정확히 중앙에 위치하는값
- 관찰값의 개수가 홀수일 때 : 중앙에 위치하는 관찰값
- 관찰값의 개수가 짝수일 때: 중앙에 위치하는 2개 관찰값의 평균
- ex ) 1, 2, 3, 4, 5, 6일 경우 중앙값 = ( 3 + 4 ) / 2 = 3.5
- 특이점의 영향을 거의 받지 않는다
- 분포가 한쪽으로 쏠려 있거나,특이점이 존재하는 데이터를 요약할 때 주로 사용된다
4. 사분위수( Quartiles )
- 크기 순서대로 늘어놓은 데이터를 4등분하는 값
- 1사분위수( Q1 ) : 전체 데이터 중 값이 낮은 1/4과 나머지를 가르는 값
- 2사분위수( Q2 ) : 전체 데이터 중 값이 낮은 2/4와 나머지를 가르는 값 = 중앙값
- 3사분위수( Q3 ) : 전체 데이터 중 값이 낮은 3/4와 나머지를 가르는 값
- 사분위수 범위( InterQuartile Range : IQR )
- 3사분위수( Q3 ) - 1사분위수( Q1 )
5. 사분위수 예제
- 학생 10명이 1분당 할 수 있는 윗몸일으키기 개수
- ex ) 8, 23, 25, 28, 32, 35, 37, 41, 42, 52
- 1사분위수 = 25
- 2사분위수 ( 중앙값 ) = ( 32 + 35 ) / 2 = 33.5
- 3사분위수 = 41
6. 백분위수 ( Percentile )
- p백분위수 : 전체 데이터의 p%가 이 값보다 작거나 같은 값
- 1사분위수 = 25 백분위수
- 2사분위수 = 50 백분위수 = 중앙값
- 3사분위수 = 75 백분위수
7. 백분위수 예제
- 생후 12개월인 여아 은지의 체중은 10kg이고 이것은 75백분위수에 해당된다고 한다
- 이는 전체 데이터의 75%는 은지보다 체중이 낮고, 25%는 은지보다 체중이 높단 의미
8. 범위
- 관찰값의 최댓값 - 최솟값
- 데이터의 산포를 설명하는 가장 간단한 통계량
- 특이점의 영향을 심하게 받는다
9. 다섯 수치요약과 상자그림
- 다섯 수치요약( five-numbersummary )
- 최솟값, 1사분위수, 중앙값, 3사분위수, 최댓값를 차례대로 나열
- 데이터의 중심위치와 퍼진 정도를 모두 파악할 수 있다
- 상자그림( boxplot )
- 다섯 수치요약을 나타낸 그래프
10. 데이터의 중심위치
- 평균
- 분포의 무게중심
- 대칭적인 분포의 경우 데이터를 잘 대표한다
- 분포가 기울어져 있거나 특이점이 있는 경우 데이터를 잘 대표하지 못한다
- 중앙값
- 데이터를 크기 순으로 정렬했을 때 가장 가운데에 위치하는 값
- 분포가 기울어져 있거나 특이점이 있는 경우 많이 쓰인다
- 최빈값
- 빈도가 가장 높은 관찰값
- 여러개 있을 수도, 하나도 없을 수도 있다
- 분포의 중심위치에서 멀리 떨어져있을 수도 있다
11. 좌우 대칭인 종모양 분포
- 평균, 중앙값, 최빈값이 비슷하다
12. 기울어진 분포
- 평균이 ( 중앙값에 비해 ) 긴 꼬리 쪽에 더 가깝게 된다
13. 쌍봉우리형 분포
- 2개의 최빈값이 관찰될 수 있다
14. 데이터의 산포
- 분산 : 편차의 제곱의 평균
- 표준편차 : 분산의 제곱근
- 범위 : 최댓값 - 최솟값
- 사분위수 범위 : 3사분위수 - 1사분위수
- 이 값들이 클 수록 데이터의 분포가 많이 퍼진 것이다
- 분산, 표준편차, 범위는 특이점의 영향을 크게 받는다
- 사분위수 범위는 특이점의 영향을 크게 받지 않는다
15. 분산과 분포 형태
- 평균이 같고 분산이 다른 두 분포
16. 그래프 - 히스토그램
- hist( )함수를 이용해서 그린다
- ex ) hist( x, breaks, main, xlab, ylab, xlim, ylim, ... )
- x : 데이터 벡터
- breaks : 계급에 대한 정보
- 계급의 개수
- 계급을 나누는 값들의 벡터
- main : 그래프의 제목
- xlab : x축 제목
- ylab : y축 제목
- xlim : x축의 범위
- ex ) xlim = c ( 최소값, 최대값 )
- ylim : y축의 범위
17. 히스토그램 예제
score <- c(93, 83, 91, 68, 75, 87, 89, 96, 97, 67, 83, 81, 87, 80, 64,
83, 88, 76, 91, 78, 72, 80, 69, 80, 84, 71, 91, 81, 88, 73)
hist(score)
hist(score, main="")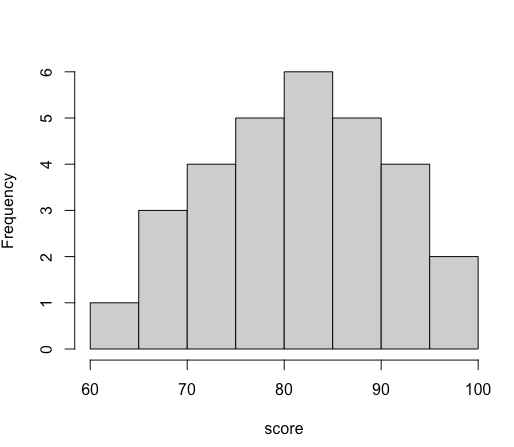
18. 히스토그램 예제 2
rv<-c(0.8, 0.8, 0.8, 0.9, 0.9, 0.9, 0.9, 0.9,
1, 1, 1.8,
2, 2.1, 2.3, 2.4, 2.8, 2.9,
3, 3.2, 3.3, 3.5, 3.8, 3.8, 3.9,
4, 4.2, 4.4, 4.5,
5.1, 5.3, 5.3, 5.4,
14, 17, 18, 19,
21, 21, 23, 25, 27, 28, 32, 34, 36,
41, 42, 44, 48, 49,
51, 54, 59, 60, 61, 62, 80,
240)
hist(rv)
hist(rv, main="", xlab="CRP", breaks=20)
## x축의 라벨을 CRP로 변경하고 계급을 20으로 나눈
hist(rv, main="", xlab="CRP", breaks=seq(0, 240, 20))
## seq를 통해서 0에서 240까지 20씩 뛰어넘는 수를 만듦
## 이를 통해서 만들어진 0 20 40 ... 240을 계급으로 하여 히스토그램 생성
19. 히스토그램 예제 3 : 계급에 따른 히스토그램 차이
## 항상 같은 난수를 만들기위해 set.seed로 고정
set.seed(2021)
## 난수발생
rn<-c(rnorm(100, 5, 2), rnorm(100, 10, 2))
#좁은 히스토그램 ( 계급이 자세함 )
hist(rn, breaks=20, main="", xlab="value")
## 넓은 히스토그램 ( 계급이 넓음 )
hist(rn, breaks=5, main="", xlab="value")
20. 상자그림
- boxplot( )함수를 이용해서 그린다
- ex ) boxplot( x, ... )
- x : 데이터 벡터
21. 상자그림 예제 1
age<-c(57, 61, 47, 57, 48, 58, 57, 61, 54, 50, 68, 51)
boxplot(age, ylab="Age")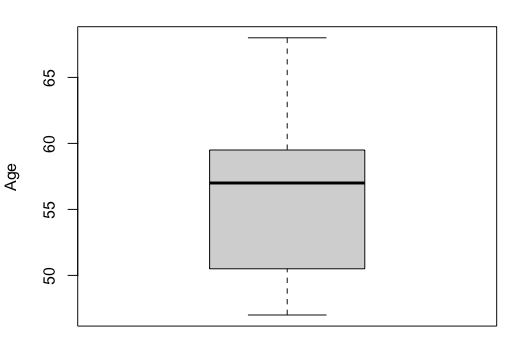
22. 상자그림 예제 2
member<-c(92, 107, 180, 90, 78, 91, 102, 88, 106, 125, 95, 102, 162)
boxplot(member, ylab="Number of board members")
## 특이점의 경우 점으로 나타낸다.
23. R에서 요약 통계량 구하는 방법
- 평균 : mean( x )
- 분산 : var( x )
- 표준편차 : sd( x )
- 중앙값 : median( x )
- 다섯수치 요약 : fivenum( x )
- 사분위수 범위 : IQR( x )
- 범위 : range( x )
24. 요약 통계량 예제
member<-c(92, 107, 180, 90, 78, 91, 102, 88, 106, 125, 95, 102, 162)
## 평균 : 109.0769
mean(member)
## 분산 : 899.0769
var(member)
## 표준편차 : 29.98461
sd(member)
## 중앙값 : 102
median(member)
## 다섯수치 요약 : 78 91 102 107 180
fivenum(member)
## 사분위수 범위 :16
IQR(member)
## 범위 : 78 180
range(member)728x90
'방송대 > R 컴퓨팅' 카테고리의 다른 글
| 5강. 데이터 구조 (2) (0) | 2025.03.23 |
|---|---|
| 4강. 데이터 구조 (1) (0) | 2025.03.15 |
| 3강. 데이터 입력과 저장 (0) | 2025.03.09 |
| 2강. R 입문 ( 2 ) (0) | 2025.03.02 |
| 1강. R 입문( 1 ) (0) | 2025.02.23 |
댓글

