티스토리 뷰
1. 알고리즘 분석
- 정확성 분석
- 유효한 입력에 대해 유한 시간 내에 정확한 결과의 생성 여부
- 수학적 기법을 사용한 이론적인 증명 과정
- 효율성 분석
- 알고리즘 수행에 필요한 컴퓨터 자원의 양을 측정 / 평가
- 공간 복잡도 ( Space Complexity )
- 메모리의 양 = 정적 공간 + 동적 공간
- 시간 복잡도 ( Time Complexity )
- 수행시간 = 알고리즘의 실행에서부터 완료까지 걸리는 시간
- 주로 알고리즘 분석은 시간 복잡도 분석을 의미
2. 시간 복잡도
- 시간 복잡도는 컴퓨터에서 실행시켜 실제 수행시간을 측정하는 방법을 의미하는가?
- 실행 환경에 종속적이므로 일반성이 결여된 방법
- 컴퓨터 속도, 구현에 사용된 프로그래밍 언어, 프로그램 작성 방법, 컴파일러의 효율성 등에 따라 시간이 달라짐 → 효율성 분석을 하는데 적합하지 X
- 알고리즘 수행시간 = ∑ { 각 문장( 연산 )이 수행되는 횟수 } ( 각 연산이 수행되는 횟수의 합 )
- 수행시간에 영향을 미치는 요인
- 입력 크기
- ex ) 입력되는 데이터의 크기, 문제가 해결하려는 대상이 되는 개체의 개수
- 입력 크기 𝑛이 커질수록 수행시간도 증가
- 단순히 단위 연산이 수행되는 개수의 합으로 표현하는 것은 부적절
- 그렇기에 입력 크기 𝑛의 함수 𝑓(𝑛)으로 표현함
- 입력 데이터의 상태
- 평균 수행시간 : 𝐴(𝑛) = ∑𝐼∈𝑆𝑛 𝑃(𝐼) 𝑡(𝐼)
- 최선 수행시간 : 𝐵(𝑛) = min𝐼∈𝑆𝑛 𝑡(𝐼)
- 최악 수행시간 : 𝑊(𝑛) = max𝐼∈𝑆𝑛𝑡(𝐼)
- 주로 알고리즘의 시간 복잡도는 최악 수행시간으로 나타낸다.
- 최악 수행시간을 기준으로 잡으면 다른 수행시간은 최악보다는 덜 걸린단걸 알 수 있기 때문이다.
- 입력 크기
- 수행시간에 영향을 미치는 요인
3. 점근성능
- 입력 크기 𝑛이 무한히 커짐에 따라 결정되는 성능
- 점근성능의 결정 방법
- 입력 크기가 충분히 커짐에 따라 함숫값에 가장 큰 영향을 미치는 차수를 찾음
- 수행시간의 다항식 함수에서 최고차항만을 계수 없이 취해서 표현
- ex ) f3(n)=2n2+5n+200
- ex 최고차항 ) 2n2 ( 2 n의 제곱 )
- ex 계수없는 최고차항 ) n2 ( n의 제곱 )
- 수행시간의 정확한 값이 아닌 어림값
- 수행시간의 증가 추세를 파악하는 것이 쉬움
- 알고리즘 간의 우열을 따질 때 유용
- 최고차항이란?
- 함수, 방정식, 부등식 등을 이루는 다항식에서 차수가 가장 높은 항
4. 점근성능의 표기법
- Big-oh 점근적 상한
- 함수 f와 g는 각각 양의 정수를 갖는 함수
- 어떤 양의 상수 c와 n0이 존재하여
- 모든 n≥n0에 대하여 f(n)≤c·g(n)이면 f(n)=O(g(n))이다.
- O(g(n))은 최악 수행시간을 의미
- Big-omega 점근적 하한
- 함수 f와 g는 각각 양의 정수를 갖는 함수
- 어떤 양의 상수 c와 n0이 존재하여
- 모든 n≥n0에 대하여 f(n)≥c·g(n)이면 f(n)=Ω(g(n))이다.
- Ω(g(n))는 최선 수행시간을 의미
- Big-theta 점근적 상하한
- 점근적 상한과 점근적 하한을 동시에 표시
- 모든 n≥n0에 대하여 **c1·g(n)≤f(n)≤c2·g(n)**이면 f(n)=Θ(g(n))이다.
- 정확학 알고리즘 수행시간을 표시한다.
5. 점근성능의 표기법
- f(n)=3n+3, g(n)=n
- O(n) / Ω(n) / Θ(n)
- f(n)=3n3+3n-1, g(n)=n3
- O(n3) / Ω(n3) / Θ(n3)
- 위와 같이 최고차항만을 계수 없이 표현
- 점근성능의 효율성은 다음과 같다.
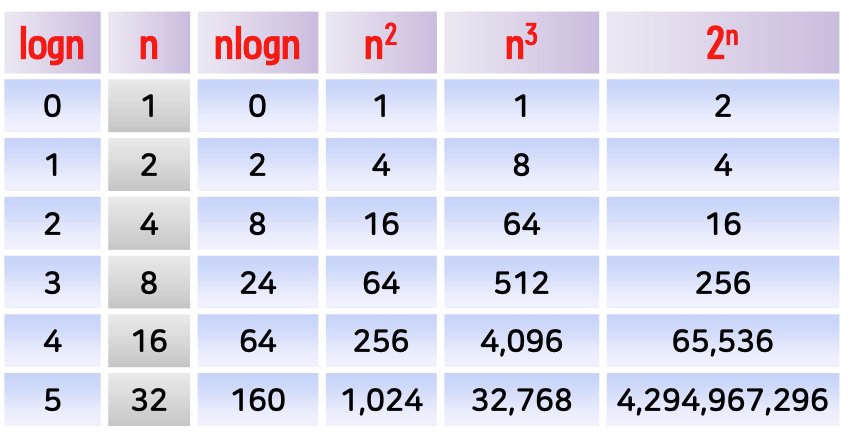
- O(1) : 상수 시간 < O(logn) : 로그 시간 < O(n) : 선형 시간 < O(nlogn) 로그 선형 시간< O(n2) : 제곱 시간 < O(n3) : 세제곱 시간 < O(2n) : 지수 시간
- 왼쪽일수록 효율적이고 오른쪽일수록 비효율적이다.
7. 순환 알고리즘 ( Recursion : 재귀 알고리즘 )
- 알고리즘의 수행 과정에서 자기 자신의 알고리즘을 다시 수행하는 형태
- 점화식으로 표현
- ex ) T(n) = T(n/2) + O(1), T(1)=c1
- 점화식의 폐쇄형을 구해야 한다.
- 기본 점화식과 폐쇄형 ( * )

8. 요약
- 알고리즘 분석
- 정확성 분석 + 효율성 분석
- 효율성 분석 → 공간 복잡도, 시간 복잡도 ( 각 문장의 수행횟수의 합 )
- 시간 복잡도 → 입력 크기의 함수와 최악의 수행시간으로 표현
- 점근성능
- 입력 크기가 무한히 커짐에 따라 결정되는 성능 → 최고차수만으로 간략히 표현
- 표기법 → O-표기, Ω-표기, Θ-표기
- O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n)
- 순환 알고리즘
- 순환 알고리즘의 수행시간은 점화식 형태로 정의되며, 폐쇄형을 구해서 표현
- 분할정복 방법이 적용된 알고리즘은 기본적으로 순환 알고리즘 형태를 가짐
- 기본 점화식과 폐쇄형
728x90
'방송대 > 알고리즘' 카테고리의 다른 글
| 6강. 탐색 (1) (0) | 2025.03.26 |
|---|---|
| 5강. 정렬 (3) (0) | 2025.03.19 |
| 4강. 정렬 ( 2 ) (0) | 2025.03.12 |
| 3강. 정렬 ( 1 ) (0) | 2025.03.05 |
| 1강. 알고리즘 소개 ( 1 ) (0) | 2025.02.23 |
댓글
